ライフプランニングの考え方・手法(6つの係数)

ライフプランニングを立てる際に、積立投資を行ったり、定年後の貯金の取り崩しなどの資金計画検討するのですが、その際に計算を簡単にするために6つの係数があります。
簡単に特徴をまとめるとこんな感じ。
| 係数の名前 | 運用方法 | 計算式(使い方) |
|---|---|---|
| 終価係数 | 定額 | 運用後金額 = 元本 × 終価係数 |
| 現価係数 | 定額 | 必要な元本 = 運用後金額 × 現価係数 |
| 年金終価係数 | 積立 | 運用後金額 = 積立金額 × 年金終価係数 |
| 減債基金係数 | 積立 | 積立金額 = 運用後金額 × 減債基金係数 |
| 資本回収係数 | 取り崩し | 取り崩し金額 = 元本 × 資本回収係数 |
| 年金現価係数 | 取り崩し | 必要な元本 = 取り崩し金額 × 年金現価係数 |
それでは、6つの係数について具体的な例で学んでいきましょう。
終価係数
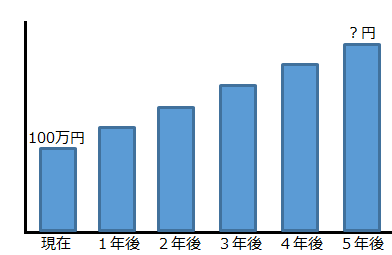
<例題>
元本100万円を年利5%で運用した場合、5年後にいくらになるか?
終価係数:1.2763
<計算式>
運用後金額 = 元本 × 終価係数
ですので、当てはめると
1,000,000円 × 1.2763 = 1,276,300円
現価係数
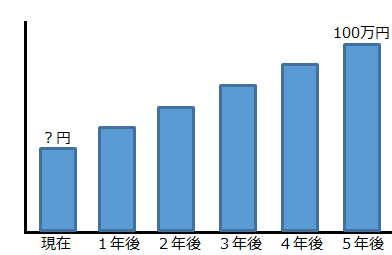
<例題>
年利5%で運用し、5年後に100万円にするためには元本はにいくら必要か?
現価係数:0.7835
<計算式>
必要な元本 = 運用後金額 × 現価係数
ですので、当てはめると
1,000,000円 × 0.7835 = 783,500円
年金終価係数
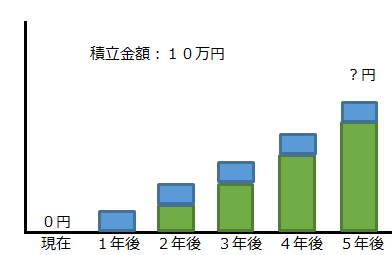
<例題>
毎年10万円を積立で年利5%で運用した場合、5年後にいくらになるか?
年金終価係数:5.5256
<計算式>
運用後金額 = 積立金額 × 年金終価係数
ですので、当てはめると
100,000円 × 5.5256 = 552,560円
減債基金係数
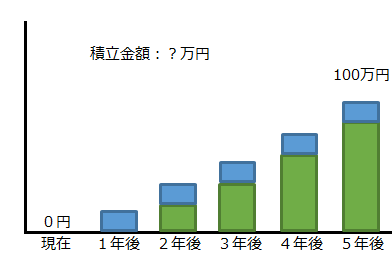
<例題>
年利5%で運用し、5年後に100万円にするためには毎年いくら積立てが必要か?
現価係数:0.1810
<計算式>
積立金額 = 運用後金額 × 減債基金係数
ですので、当てはめると
1,000,000円 × 0.1810 = 181,000円
資本回収係数
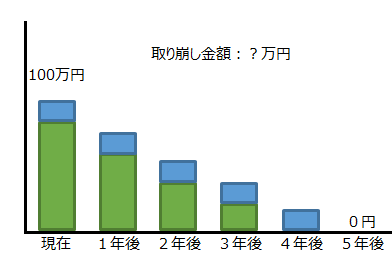
<例題>
100万円を年利5%で運用しながら5年間で取り崩した場合、毎年の取り崩し金額はいくらになるか?
資本回収係数:0.2310
<計算式>
取り崩し金額 = 元本 × 資本回収係数
ですので、当てはめると
1,000,000円 × 0.2310 = 231,000円
年金現価係数
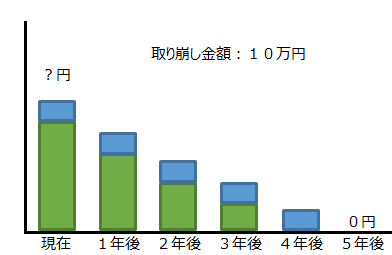
<例題>
毎年10万円を年利5%で運用しながら5年間で取り崩す場合 、元本はいくら必要か?
年金現価係数:4.3295
<計算式>
必要な元本 = 取り崩し金額 × 年金現価係数
ですので、当てはめると
100,000円 × 4.3295 = 432,950円








